El teorema de Napoleón y sus teorías

El teorema de Napoleón es un resultado geométrico que lleva el nombre del famoso emperador francés Napoleón Bonaparte. Este teorema establece una relación interesante entre los triángulos equiláteros construidos externamente en los lados de cualquier triángulo.

El teorema de Napoleón afirma que si construimos triángulos equiláteros externamente en los lados de un triángulo dado, entonces los centros de estos triángulos forman un triángulo equilátero. En otras palabras, si etiquetamos los vértices del triángulo original como A, B y C, y construimos triángulos equiláteros externamente en los lados AB, BC y CA, entonces los centros de estos triángulos formarán un triángulo equilátero.

El teorema de Napoleón ha sido objeto de numerosas teorías y generalizaciones a lo largo de los años. Algunas de estas teorías incluyen la relación entre el teorema de Napoleón y el teorema de Morley, que establece una relación entre los triángulos equiláteros construidos internamente en los ángulos de cualquier triángulo. Otra teoría interesante es la conexión entre el teorema de Napoleón y la geometría fractal, que estudia las formas irregulares y autosimilares.

El teorema de Napoleón y sus teorías han sido objeto de estudio y fascinación para matemáticos y aficionados a la geometría en todo el mundo. Esta relación entre los triángulos equiláteros y la formación de un triángulo equilátero a partir de los centros de estos triángulos externos es un ejemplo fascinante de la belleza y la elegancia de las matemáticas.

El teorema establece lo siguiente: Dado cualquier triángulo, si se construyen triángulos equiláteros en el exterior de cada uno de sus lados, entonces los centros de estos triángulos equiláteros formarán un triángulo equilátero.

Para visualizar esto, sigue estos pasos:

1. Dibuja un triángulo cualquiera. Los puntos A, B y C son los vértices de tu triángulo.
2. En el exterior de cada uno de los lados del triángulo original, construye triángulos equiláteros. Esto significa que desde el punto A, traza un triángulo equilátero fuera del lado BC. Desde el punto B, traza un triángulo equilátero fuera del lado CA. Y desde el punto C, traza un triángulo equilátero fuera del lado AB.
3. Los centros de estos tres triángulos equiláteros (denotados como D, E y F) formarán un triángulo equilátero.

El Teorema de Napoleón se basa en las propiedades de los triángulos equiláteros y se puede demostrar utilizando geometría básica. Es un ejemplo interesante de cómo las propiedades geométricas pueden conducir a resultados sorprendentes y hermosos. 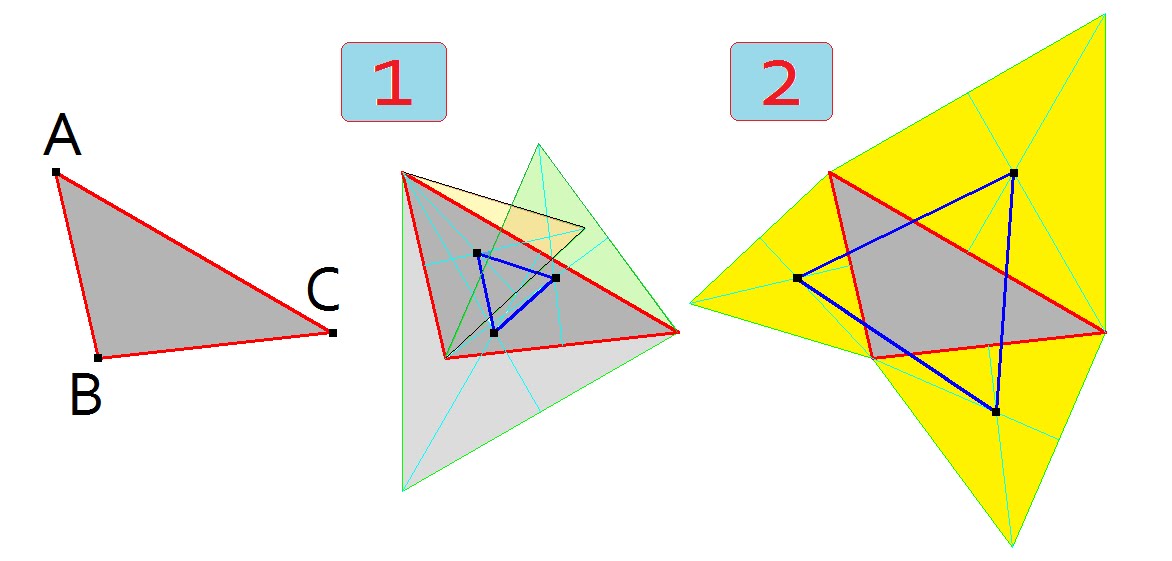Este teorema también es relevante en matemáticas y geometría, y es un tema de estudio en cursos de geometría y trigonometría.